segunda-feira, 2 de julho de 2012
terça-feira, 10 de abril de 2012
Atividade do grupo PCLKS
1. Sabendo-se que o lado de um quadrado mede 8 cm,
calcule o seu perímetro.
R: o perímetro do quadrado é 32 cm.
2. Um retângulo possui as seguintes dimensões, 5 cm de
base e 3 cm de altura.Determine o seu perímetro.
R: o perímetro deste retângulo é 16 cm
3. Determine o perímetro de um retângulo, sabendo que a
base mede 24 cm e sua altura mede a metade da base.
R: altura desse retângulo equivale 12 cm e seu perímetro
é 72 cm.
4. A praça de uma cidade possui a forma de um quadrado.
Calcule quantos metros de corda deverá ser gasto para cercar a praça para uma
festa sabendo que possui 45 m de lado, deseja-se dar Quatro voltas com a corda.
R: deverá ser gasto 720 m de corda para cercar a praça.
5. Para o plantio de laranja em todo o contorno de um
terreno retangular de 42 m x 23m. Se entre os pés de laranjas a distância é de
2,60 m, quantos pés de laranjas foram plantados?
R: foram plantados 50 pés de laranjas no terreno
retangular.
6. O perímetro de um triângulo eqüilátero corresponde a
5/6 do perímetro de um quadrado que tem 9 cm de lado. Qual é a medida, em
metros, do lado desse triângulo eqüilátero?
R: medida do lado do triângulo eqüilátero é 10 cm.
7. Numa sala quadrada, foram gastos 24,80 m de rodapé de
madeira. Essa sala tem apenas uma porta de 1,20 m de largura. Considerando que
não foi colocado rodapé na largura da porta, calcule a medida de cada lado
dessa sala.
R: cada lado ou parede dessa sala quadrada tem 6,2 m nos
três lados e tal na parede que colocará a porta tem 5 m pelo fato da largura da
porta ser 1,20 m.
8. Com 32,40 m de tecido, um comerciante quer formar 20
retalhos de mesmo comprimento. Qual o comprimento de cada retalho em
centímetros?
R: cada retalho tem comprimento de 1,62 m tal em
centímetros ficará 162 cm que é a conclusão do comerciante tem que ter.
9. O terreno de uma escola é retangular, com 100 m de
comprimento por 65 m de largura. Em todo o contorno desse terreno será plantada
árvores distantes 1,50 m uma da outra. Quantas: árvores serão necessárias?
R: será necessário plantarem 220 árvores neste terreno da
escola.
10. Um campo de futebol possui as seguintes dimensões,
155 m de comprimento e 75m de largura. Quanto metro de tela será necessário
para cercar este campo.
R: serão necessários
460 metros de tela para cercar o campo de futebol.
segunda-feira, 9 de abril de 2012
segunda-feira, 2 de abril de 2012
Quarto um:
0,0028km/0,028hm/0,28dam/28dm/280cm/2800mm.
0,0034km/0,034hm/0,34dam/34dm/340cm/3400mm.
Banho um:
0,0013km/0,013hm/0,13dam/13dm/130cm/1300mm.
0,00275km/0,0275hm/0,275dam/27,5dm/275cm/2750mm.
Quarto dois
0,0028km/0,028hm/0,28dam/28dm/280cm/2800mm.
0,00275km/0,0275hm/0,275dam/27,5dm/275cm/2750mm.
Hall:
0,0032km/0,032hm/0,32dam/32dm/320cm/3200mm.
0,0009km/0,009hm/0,09dam/9dm/90cm/900mm.
Suíte:
0,0029km/0,029hm/0,29dam/29dm/290cm/2900mm.
0,0034km/0,034hm/0,34dam/34dm/340cm/3400mm.
0,0014km/0,014hm/0,14dam/14dm/140cm/1400mm.
0,00185km/0,0185hm/0,185dam/18,5dm/185cm/1850mm.
Salão:
0,0034km/0,034hm/0,34dam/34dm/340cm/3400mm.
0,006km/0,06hm/0,6dam/60dm/600cm/6000mm.
Banho dois:
0,0013km/0,013hm/0,13dam/13dm/130cm/1300mm.
0,0024km/0,024hm/0,24dam/24dm/240cm/2400mm.
Cozinha:
0,0024km/0,024hm/0,24dam/24dm/240cm/2400mm.
0,0019km/0,019hm/0,19dam/19dm/190cm/1900mm.
0,0038km/0,038hm/0,38dam/38dm/380cm/3800mm.
Área de serviço:
0,0019km//0,019hm/0,19dam/19dm/190cm/1900mm.
0,0019km/0,019hm/0,19dam/19dm/190cm/1900mm.
Varanda:
0,002km/0,02hm/0,2dam/20dm/200cm/2000mm.
0,0085km/0,085hm/0,85dam/85dm/850cm/8500mm.
Extensão
0,01045km/0,1045hm/1,045dam/104,5dm/1045cm/10450mm.
0,00915km/0,0915hm/0,915dam/91,5dm/915cm/9150mm.
segunda-feira, 26 de março de 2012
1) Efetue as operações indicadas abaixo. Dê a resposta da 1ª operação em m e a 2ª em m².
1ª ) 3,020 m + 0,0012 km + 320 cm= 7,420 metros
2ª ) 4,33 m x 50,2 cm = 2,17366 metros quadrados
2) Transforme em quilômetros:
a) 3600 m = 3,6 km
b) 2160000 cm = 2,16 km
c) 0,03 m = 0, 00003 km
d) 27600 m = 27,6 km
e) 5800 mm = 0, 0058 km
Reflexão sobre o texto
“O problema de um é problema de todos quando convivemos
em equipe.”
Esse texto nos faz refletir de acordo com as idéias que
nos chega ao pensamento, nos fazendo criar uma idéia diferente e talvez até uma
idéia superficial.
No nosso cotidiano nos vemos submetidos a varias
situações que nos levam a trabalhar em grupos convivendo com diferenças de
nossos colegas de trabalhos, mas o trabalho em equipe é importante devido a
convivência com pessoas de diferentes jeitos e maneiras.
A pessoas que não conseguem trabalhar em grupo, devido a
timidez entre outros motivos, que no futuro acaba ocasionando uma dificuldade
de relacionamento com outras pessoas.
2)=EXERCICIO
Aproveitando uma promoção de uma loja de materiais para construção, uma família resolve trocar o piso da sala de sua residência. Sabem que a sala mede 4 metros de largura e possui um comprimento de 5,5 metros. Sabem também que o ladrilho desejado é quadrado, com 25 cm de lado. Quantos ladrilhos serão necessários para ladrilhar o piso da sala inteira? R= 352 LADRILHOS. Porque a área da sala é 22 metros quadrados, o ladrilho tem 25 centímetros fica com área de 625 centímetros quadrados tem que transforma para metros quadrados tornando-se 0, 625 metros quadrados. O valor da área dividiu-se com área do ladrilho 22metros quadrados/ 0, 625 metros quadrados igual 352 ladrilhos
Responda:
Para dificultar o trabalho dos falsificadores, foi lançada uma nova família de cédulas do real. Com tamanho variável - quanto maior o valor, maior a nota - o dinheiro novo terá diversos elementos de segurança. A estréia será entre abril e maio, quando começar a circular as novas notas de R$ 50,00 e R$ 100,00.
As cédulas atuais têm 14 cm de comprimento e 6,5 de largura. A maior cédula será a de R$ 100,00, com 1,6 cm a mais no comprimento e 0,5 cm a mais na largura.
Quais serão as dimensões da nova cédula de R$ 100,00?
a) 15,6 cm de comprimento e 6 cm de largura
b) 15,6 cm de comprimento e 6,5 cm de largura
c) 15,6 cm de comprimento e 7 cm de largura
d) 15,9 cm de comprimento e 6,5 cm de largura
e) 15,9 cm de comprimento e 7 cm de largura
1-exercicio
-fazer no paint os desenhos dos ângulos agudo, obtuso, raso e reto.
2- exercício desenhe no paint os seguintes ângulos :
a)32° h)115°
b)57° i)170°
c)111° j)100°
d)179° l)14°
e)120° m)40°
f)30°
g)45°
3- exercício
-calcule quantos graus vai dar
A)11°+ 22°-10° . 3 =
B)90°-45°. 2+ 30°=
C)57°-27° + 15° : 9=
D)180°-90° . 2 -30° + 2°=
E)360°:4 :2 : 5 =
F)270°:3 + 1°+ 9° -10°+ 7°=
PESQUISAR
1- O que são ângulos complementares?
2- O que são ângulos suplementares?
3- Quais são os ângulos notáveis e seu valores?
-fazer no paint os desenhos dos ângulos agudo, obtuso, raso e reto.
2- exercício desenhe no paint os seguintes ângulos :
a)32° h)115°
b)57° i)170°
c)111° j)100°
d)179° l)14°
e)120° m)40°
f)30°
g)45°
3- exercício
-calcule quantos graus vai dar
A)11°+ 22°-10° . 3 =
B)90°-45°. 2+ 30°=
C)57°-27° + 15° : 9=
D)180°-90° . 2 -30° + 2°=
E)360°:4 :2 : 5 =
F)270°:3 + 1°+ 9° -10°+ 7°=
PESQUISAR
1- O que são ângulos complementares?
2- O que são ângulos suplementares?
3- Quais são os ângulos notáveis e seu valores?
terça-feira, 13 de março de 2012
segunda-feira, 12 de março de 2012
1) Quanto vale em metros:
a) 3,6 km + 450 m=4,05hm
b) 6,8 hm - 0,34 dam=6,46hm
c) 16 dm + 54,6 cm + 200mm=2,346m
d) 2,4 km + 82 hm + 12,5 dam=3,345m
e) 82,5 hm + 6 hm=8850
2) Uma corda tem 9,3 m de comprimento. Quero cortá-la em 30 pedaços do mesmo tamanho. Quantos centímetros deve medir cada pedaço?R: 31 pedaços
3) Desejo emoldurar um quadro com comprimento 85 cm e largura 50 cm. Quanto custará emoldurá-lo se o metro de moldura custa R$ 120,00?R: 324,00 reais.
4) Qual dos polígonos tem maior perímetro: um triângulo eqüilátero de 7 cm de lado, um quadrado de 5 cm de lado ou um hexágono regular de 4 cm de lado?R: é o hexágono porque tem o maior perímetro de 24 cm quanto o triângulo 21 cm e quadrado de 20 cm.
5) Um comerciante foi multado em sua loja de tecido, pois tinha utilizado um “metro” que tinha, na realidade, 97 cm de comprimento. Se até aquele momento ele havia vendido 245 “metros” de tecido, em quantos metros a sua clientela foi lesada?R:7,35 metros.
6) A distância entre duas cidades, nos Estados Unidos, é 200 milhas. Qual é essa distância, em quilômetros, sabendo que 1 milha terrestre vale, aproximadamente, 1,609 km?
R: 321,800 km de distância das duas cidades.
7) Uma corrida tem um percurso de 12,4 km de extensão, e um corredor já completou 3/4 do seu total. Quantos metros faltam para esse atleta terminar a corrida?R: Falta 3,1 metros para terminar a corrida
Figuras geométricas
Figuras geométricas são figuras de varias formas que estão presentes em nossas vidas.Seja qualquer objeto,qualquer figura...
segunda-feira, 5 de março de 2012
Faça as devidas transformações:
a)5,81 km em hm = 58,1hm
b)12,3 m em DM = 123 dm
c) 7 hm em dam = 70 dam
d)1,52 m em cm = 152 cm
e) 18,2 dm em mm =1820 mm
f) 0,01 hm em dam = 0,1 dam
g)5 km em m = 5000 m
h)0,125 m em cm = 12,5 cm
i)14,75 cm em mm = 147,5 mm
j)1,9 m em mm = 1900mm
2. Faça as transformações:
a) 32,8 dm em m =3,28 m
b) 15 mm em cm =1,5 cm
c) 187,9 m em dam = 18,79 dam
d) 540 dm em km =5,40 km
e)75,85 cm em DM = 7,585 dm
f) 1,9 dam em hm = 0,19 hm
g)0,12 m em dam = 0,012 dam
h)8500 mm em m = 8,5 m
i) 0,5 dm em m =0,05 m
j)170 m em km = 0,17 km
3. Faça as transformações: :
a)43 m em dm =
b) 74,1 hm em dam = 7,41 dam
c)0,18 cm em mm = 1,8mm
d) 15 dm em cm = 150cm
e) 1,05 dam em m =10,5 m
f) 17,3 dm em m =1,73 m
g)5,708 m em mm = 5708 mm
h)27 m em cm = 2700 cm
i) 16 m em dam = 160 dam
J)0,05 m em mm = 50 mm
4. Transforme em metros.
a) 7 km=7000m b) 0,03 dam=0,3m c) 98 cm=0,98 d) 1 dm=0,1m
5. Calcule o valor das seguintes expressões dando a resposta em metros:Obs: é necessário transformar cada medida em uma mesma unidade (neste exercício,
em metros) antes de efetuar as operações.
a) 35 dm +13 m = 13,35m
b)300 cm + 1,8 dam = 3.18 m
c) 0,12 dam + 18 dm =38,2m
d)3,2 km – 170 dm + 12 m =4230m
e) 0,38 km + 32 dm + 12 dam =522m
f) 1,2 dam +0,03 km – 140 dm =38,0m 0,43 dm
a)
b)
c) 7 hm em dam = 70 dam
d)
e) 18,2 dm em mm =
f) 0,01 hm em dam = 0,1 dam
g)
h)
i)
j)
2. Faça as transformações:
a) 32,8 dm em m =
b) 15 mm em cm =
c) 187,9 m em dam = 18,79 dam
d) 540 dm em km =
e)
f) 1,9 dam em hm = 0,19 hm
g)
h)
i) 0,5 dm em m =
j)
3. Faça as transformações: :
a)
b) 74,1 hm em dam = 7,41 dam
c)
d) 15 dm em cm = 150cm
e) 1,05 dam em m =
f) 17,3 dm em m =
g)
h)
i) 16 m em dam = 160 dam
J)
4. Transforme em metros.
a) 7 km=7000m b) 0,03 dam=0,3m c) 98 cm=0,98 d) 1 dm=0,1m
5. Calcule o valor das seguintes expressões dando a resposta em metros:Obs: é necessário transformar cada medida em uma mesma unidade (neste exercício,
em metros) antes de efetuar as operações.
a) 35 dm +
b)
c) 0,12 dam + 18 dm =38,2m
d)
e) 0,38 km + 32 dm + 12 dam =522m
f) 1,2 dam +
Surgimento e a aplicação nos dias de hoje da Geometria
A geometria é a parte da matemática cujo objeto de estudo é o espaço e as figuras que podem ocupá-lo. A partir da experiência, ou, eventualmente, intuitivamente, as pessoas caracterizam o espaço por certas qualidades fundamentais, que são denominadas axiomas de geometria (como, por exemplo, os axiomas de Hilbert). Esses axiomas não são provados, mas podem ser usados em conjunto com os conceitos matemáticos de ponto, linha reta, linha curva, superfície e sólido para chegar a conclusões lógicas, chamadas de teoremas.
A influência da geometria sobre as ciências físicas foi enorme. Como exemplo, quando o astrônomo Kepler mostrou que as relações entre as velocidades máximas e mínimas dos planetas, propriedades intrínsecas das órbitas, estavam em razões que eram harmônicas — relações musicais —, ele afirmou que essa era uma música que só podia ser percebida com os ouvidos da alma — a mente do geômetra.
A matemática surgiu de necessidades básicas, em especial da necessidade econômica de contabilizar diversos tipos de objetos. De forma semelhante, a origem da geometria (do grego geo =terra + metria= medida, ou seja, "medir terra") está intimamente ligada à necessidade de melhorar o sistema de arrecadação de impostos de áreas rurais, e foram os antigos egípcios que deram os primeiros passos para o desenvolvimento da disciplina.
Todos os anos o rio Nilo extravasava as margens e inundava o seu delta. A boa notícia era a de que as cheias depositavam nos campos de cultivo lamas aluviais ricas em nutrientes, tornando o delta do Nilo a mais fértil terra lavrável do mundo antigo. A má notícia consistia em que o rio destruía as marcas físicas de delimitação entre as possessões de terra. Dessa forma, avidam daí conflitos entre indivíduos e comunidades sobre o uso dessa terra não delimitada.
A dimensão desses conflitos pode ser apreciada na repercussão que se encontra no Livro dos Mortos do Egito, onde uma pessoa acabada de falecer tem de jurar aos deuses que não enganou o vizinho, roubando-lhe terra. Era um pecado punível com ter o coração comido por uma besta horrível chamada o «devorador». Roubar a terra do vizinho era considerado uma ofensa tão grave como quebrar um juramento ou assassinar alguém. Sem marcos fronteiriços, os agricultores e administradores de templos, palácios e demais unidades produtivas fundadas na agricultura não tinham referência clara do limite das suas possessões para poderem cultivá-la e pagarem os impostos devidos na medida da sua extensão aos governantes.
Os antigos faraós resolveram passar a nomear funcionários, os agrimensores, cuja tarefa era avaliar os prejuízos das cheias e restabelecer as fronteiras entre as diversas posses. Foi assim que nasceu a geometria. Estes agrimensores, ou esticadores de corda (assim chamados devido aos instrumentos de medida e cordas entrelaçadas concebidas para marcar ângulos retos), acabaram por aprender a determinar as áreas de lotes de terreno dividindo-os em retângulos e triângulos.
Acredita-se em geral que a origem da geometria se situa no Egito, o que é natural, pois, para a construção das pirâmides e outros monumentos desta civilização, seriam necessários conhecimentos geométricos. Estudos mais recentes contrariam esta opinião e referem que os egípcios foram buscar aos babilónios muito do seu saber.
Geometria plana: a: intuição refere-se ao aspecto imaginativo, a capacidade ou a habilidade de pensar, esses aspectos citados sem sua importância no desenvolvimento do conhecimento geométrico.
A geometria plana esta relacionada diretamente a Grécia antiga em homenagem ao Euclides (grande matemático), seus teoremas que estudam as definições que estruturam a construção de varias formas planas.
A geometria plana esta apoiada sobre alguns postulados, axiomas, definições são usados para demonstrar a qualidade de cada teorema. São objetos aceitos sem demonstração, você deve aceitar conceitos para funcionar na pratica, essa geometria permite que façamos conceitos elementares para construções de objetos.
Geometria espacial: na geometria espacial estudamos as figuras que possuem, mas de duas dimensões. Essas figuras recebem os nomes de sólidos geométricos ou figuras geométricas são mais conhecidas como: prisma, pirâmides, cone, cilindro, esfera.
Exemplos:
Prisma: caixa de sapato, caixa de fósforos
Cone: casquinha de sorvete.
Cilindro: cano de PVC, canudo.
Esfera: bola de isopor, bola de futebol.
São figuras que ocupam o mesmo lugar no espaço, a geometria responsável pelo calculo do volume dessas figuras.
Brasil: um país com desemprego?
Nos dias de hoje a um grande número de desemprego no Brasil, essa é a realidade de jovens que sonham com o primeiro emprego, mas na maioria das vezes os mesmos não possuem uma qualificação profissional devido à falta de interesse e/ ou a falta de oportunidades.
O Brasil nos dias de hoje oferece cursos técnicos e profissionalizantes a jovens que sonham em ter uma boa carreira profissional, mas muitas vezes estes cursos têm um alto custo monetário que muitas vezes é difícil de paga.
Os jovens com baixa renda não possuem uma boa qualificação, o que os impede de conseguir um bom emprego, outros jovens preferem estudar e fazer concursos públicos para todas as áreas em questão, a alta quantidade de jovens em relação ao alto índice de desemprego é altíssima. Mas só os que estudam e tem um bom currículo profissional tem as melhores vagas de emprego.
quinta-feira, 1 de março de 2012
Curriculum vitae nas redes sociais
Nos dias de hoje os sites de relacionamentos ou redes sociais, além de virar uma ferramenta de criar círculos de amizades e também na vida social. Tal mercado de trabalho está presente neste universo, como investigar os futuros candidatos a entrevistas de ocupação nas suas empresas pelo outro lado as pessoas que buscam se encaixar nas vagas tem que esta por dentro do conhecimento.
Com a inovação trazida pelo Orkut, Facebook e Twitter os especialistas em recursos humanos optaram e utilizam estes sites para conhecer profundamente os futuros funcionários, procurando através de e-mail ou nome inteiro, basta um segundo se ver toda a vida do indivíduo ou a ideologia, dependendo que cada um expõe seus sentimentos na internet. Portanto o profissional de RH tem que escolhe a pessoa possa se enquadra o padrão do estabelecimento e também da sua opinião.
O desempregado ou iniciante ao mercado de trabalho que é usuário desse tipo de site, deve se preocupar com o seu próprio perfil como aparência pessoal, cuidando não se expor seus comportamentos íntimos, por exemplo: postar fotos de amigos na praia bebendo cerveja, poesias de dor sentimental e participar de comunidades de ódio alheio. São alguns pontos negativos que os psicólogos ou recrutadores dispensam para entrevista.
As redes sociais entretêm o mundo todo e também tem que saber utilizar corretamente para não se excluir no convívio social e no mercado de trabalho. Portanto os responsáveis de recruta pessoas a empresas se baseiam o conteúdo dos perfis das redes sociais apresentados e criados por si mesmos, então cuidados o que colocar em sua pagina pessoal em informação positiva ou negativa.
Geometria Plana e Espacial
GEOMETRIA PLANA
A geometria plana, também chamada geometria elementar ou Euclidiana, teve início na Grécia antiga. Esse estudo analisava as diferentes formas de objetos, e baseia-se em três conceitos básicos: ponto, reta e plano. O conceito de ponto é um conceito primitivo, pois não existe uma definição aceita de ponto, temos nesse caso que aceitar sua existência e indicaremos um ponto por uma letra maiúscula do alfabeto(A, G, P,. . . ). Podemos definir uma reta como sendo um número infinito de pontos em sequência. Não é difícil perceber que sobre um ponto passa um número infinito de retas, porém sobre dois pontos distintos passa apenas uma reta distinta.
Uma reta que apenas passa por estes dois pontos é chamada de reta infinita, caso ela comece em um ponto qualquer e não tenha fim, ela será denominada reta semi-infinita, e no caso de ela se iniciar em um ponto e terminar em um outro ela será denominada de semi-reta. Indicaremos uma reta por uma letra minúscula qualquer (r,s,t,. . . ). Se tivermos três pontos distintos, teremos então um plano o qual contém os três pontos e todas as retas que passarem por dois destes pontos estarão contidas no plano, assim como também estarão contidas no plano todas as retas paralelas às retas citadas anteriormente. Indicaremos um plano por uma letra minúscula do alfabeto grego (a, b, g, ...).
Para saber relacionar no espaço as retas entre si temos que saber quais suas posições relativas, o que pode ser feito usando-se a definição de ângulo: O ângulo geométrico é dado pela união de duas retas não colineares(que estão na mesma linha) partindo da mesma origem. O ângulo entre estas duas retas é medido em graus, de tal forma que caibam 180° em uma circunferência completa. Depois de conhecermos estes conceitos, poderemos introduzir as definições das formas geométricas mais utilizadas, uma delas é o triângulo, que consiste na reunião de três segmentos de reta cujas extremidades se encontram sobre pontos não colineares. Chamamos de lado oposto a um certo ângulo interno ao triângulo o segmento de reta que une os outros dois ângulos do triângulo e lados adjacentes a um ângulos os segmentos de reta que partem deste ângulo. Chamamos também de ângulo externo de um triângulo ao ângulo que é ao mesmo tempo adjacente e suplementar a algum de seus ângulos internos.
Os triângulos podem ser classificados em diversos tipos de acordo com seus lados(Equiláteros - Possuem três lados de mesmo comprimento, Isósceles - possuem dois lados de mesmo comprimento e Escalenos - possuem três lados de comprimentos diferentes) ou quanto a seus ângulos(Retângulos - possuem um ângulo de 90° graus, também chamado ângulo reto, Obtusângulos - possuem um ângulo obtuso, ou seja, um ângulo com mais de 90°, Acutângulos - possuem três ângulos agudos, ou seja, menores do que 90°). Polígonos são definidos como a figura formada po um número n maior ou igual a 3 de pontos ordenados de forma que três pontos consecutivos sejam não colineares.
Um exemplo de polígono de 3 lados é um triângulo. Os polígonos possuem denominações particulares para enes diferentes:n=3 - triângulo, n=4 - quadrilátero, n=10 - decágono, n=20 - icoságono). Estas denominações são derivadas dos nomes dos números em grego. Outra forma importante da geometria plana é a circunferência definida como sendo o conjunto de todos os pontos de um plano cuja distância a um ponto fixo desse plano é uma constante positiva. Chamamos de círculo ao conjunto de uma circunferência e seus pontos internos. Existem também certos casos especiais para quadriláteros como definiremos a seguir: é dado o nome de trapézio a um quadrilátero que possui dois lados paralelos.
Para o caso dos lados não paralelos serem congruentes dá-se a este trapézio o nome de trapézio isósceles, para o caso de lados não paralelos não congruentes é dado o nome de trapézio escaleno, e um trapézio que possui um lado perpendicular as bases é chamado trapézio retângulo. Paralelogramo é um quadrilátero que possui os lados opostos paralelos. Retângulo possui quatro ângulos congruentes entre si. O losango possui quatro lados congruentes entre si, e finalmente o quadrado que possui 4 lados e quatro ângulos congruentes entre si.
GEOMETRIA ESPACIAL
A Geometria espacial (euclidiana) funciona como uma ampliação da Geometria plana (euclidiana) e trata dos métodos apropriados para o estudo de objetos espaciais assim como a relação entre esses elementos. Os objetos primitivos do ponto de vista espacial, são: pontos, retas, segmentos de retas, planos, curvas, ângulos e superfícies. Os principais tipos de cálculos que podemos realizar são: comprimentos de curvas, áreas de superfícies e volumes de regiões sólidas. Tomaremos ponto e reta como conceitos primitivos, os quais serão aceitos sem definição.
Conceitos gerais
Um plano é um subconjunto do espaço R3 de tal modo que quaisquer dois pontos desse conjunto pode ser ligado por um segmento de reta inteiramente contido no conjunto.
Um plano no espaço R3 pode ser determinado por qualquer uma das situações:
Duas retas são ditas reversas quando uma não tem interseção com a outra e elas não são paralelas. Pode-se pensar de uma rera r desenhada no chão de uma casa e uma reta s desenhada no teto dessa mesma casa.
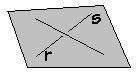
Uma reta é perpendicular a um plano no espaço R3, se ela intersecta o plano em um ponto P e todo segmento de reta contido no plano que tem P como uma de suas extremidades é perpendicular à reta.
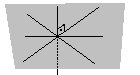
Uma reta r é paralela a um plano no espaço R3, se existe uma reta s inteiramente contida no plano que é paralela à reta dada.
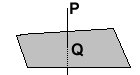
Seja P um ponto localizado fora de um plano. A distância do ponto ao plano é a medida do segmento de reta perpendicular ao plano em que uma extremidade é o ponto P e a outra extremidade é o ponto que é a interseção entre o plano e o segmento.
Se o ponto P estiver no plano, a distância é nula.
Planos concorrentes no espaço R3 são planos cuja interseção é uma reta. Planos paralelos no espaço R3 são planos que não tem interseção.
Quando dois planos são concorrentes, dizemos que tais planos formam um diedro e o ângulo formado entre estes dois planos é denominado ângulo diedral. Para obter este ângulo diedral, basta tomar o ângulo formado por quaisquer duas retas perpendiculares aos planos concorrentes.
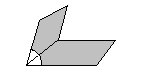
Planos normais são aqueles cujo ângulo diedral é um ângulo reto (90 graus).
Conceitos geométricos primitivos
A Geometria Plana e a Geometria Espacial baseiam-se nos chamados conceitos geométricos primitivos. Define-se como conceito primitivo toda aquele que não admite definição, isto é, o conceito que é aceito por ser óbvio ou conveniente para uma determinada teoria. Normalmente, em Matemática, os conceitos primitivos servem de base para a construção de postulados (ou axiomas) que formarão, por sua vez, a estrutura lógica e formal da teoria.
Ao contrário do que se pensa, conceitos primitivos existem não somente em Matemática, mas em fisica também. Exemplos desses conceitos são os conceitos de força e velocidade.
Os conceitos geométricos primitivos são os seguintes:
A geometria plana, também chamada geometria elementar ou Euclidiana, teve início na Grécia antiga. Esse estudo analisava as diferentes formas de objetos, e baseia-se em três conceitos básicos: ponto, reta e plano. O conceito de ponto é um conceito primitivo, pois não existe uma definição aceita de ponto, temos nesse caso que aceitar sua existência e indicaremos um ponto por uma letra maiúscula do alfabeto(A, G, P,. . . ). Podemos definir uma reta como sendo um número infinito de pontos em sequência. Não é difícil perceber que sobre um ponto passa um número infinito de retas, porém sobre dois pontos distintos passa apenas uma reta distinta.
Uma reta que apenas passa por estes dois pontos é chamada de reta infinita, caso ela comece em um ponto qualquer e não tenha fim, ela será denominada reta semi-infinita, e no caso de ela se iniciar em um ponto e terminar em um outro ela será denominada de semi-reta. Indicaremos uma reta por uma letra minúscula qualquer (r,s,t,. . . ). Se tivermos três pontos distintos, teremos então um plano o qual contém os três pontos e todas as retas que passarem por dois destes pontos estarão contidas no plano, assim como também estarão contidas no plano todas as retas paralelas às retas citadas anteriormente. Indicaremos um plano por uma letra minúscula do alfabeto grego (a, b, g, ...).
Para saber relacionar no espaço as retas entre si temos que saber quais suas posições relativas, o que pode ser feito usando-se a definição de ângulo: O ângulo geométrico é dado pela união de duas retas não colineares(que estão na mesma linha) partindo da mesma origem. O ângulo entre estas duas retas é medido em graus, de tal forma que caibam 180° em uma circunferência completa. Depois de conhecermos estes conceitos, poderemos introduzir as definições das formas geométricas mais utilizadas, uma delas é o triângulo, que consiste na reunião de três segmentos de reta cujas extremidades se encontram sobre pontos não colineares. Chamamos de lado oposto a um certo ângulo interno ao triângulo o segmento de reta que une os outros dois ângulos do triângulo e lados adjacentes a um ângulos os segmentos de reta que partem deste ângulo. Chamamos também de ângulo externo de um triângulo ao ângulo que é ao mesmo tempo adjacente e suplementar a algum de seus ângulos internos.
Os triângulos podem ser classificados em diversos tipos de acordo com seus lados(Equiláteros - Possuem três lados de mesmo comprimento, Isósceles - possuem dois lados de mesmo comprimento e Escalenos - possuem três lados de comprimentos diferentes) ou quanto a seus ângulos(Retângulos - possuem um ângulo de 90° graus, também chamado ângulo reto, Obtusângulos - possuem um ângulo obtuso, ou seja, um ângulo com mais de 90°, Acutângulos - possuem três ângulos agudos, ou seja, menores do que 90°). Polígonos são definidos como a figura formada po um número n maior ou igual a 3 de pontos ordenados de forma que três pontos consecutivos sejam não colineares.
Um exemplo de polígono de 3 lados é um triângulo. Os polígonos possuem denominações particulares para enes diferentes:n=3 - triângulo, n=4 - quadrilátero, n=10 - decágono, n=20 - icoságono). Estas denominações são derivadas dos nomes dos números em grego. Outra forma importante da geometria plana é a circunferência definida como sendo o conjunto de todos os pontos de um plano cuja distância a um ponto fixo desse plano é uma constante positiva. Chamamos de círculo ao conjunto de uma circunferência e seus pontos internos. Existem também certos casos especiais para quadriláteros como definiremos a seguir: é dado o nome de trapézio a um quadrilátero que possui dois lados paralelos.
Para o caso dos lados não paralelos serem congruentes dá-se a este trapézio o nome de trapézio isósceles, para o caso de lados não paralelos não congruentes é dado o nome de trapézio escaleno, e um trapézio que possui um lado perpendicular as bases é chamado trapézio retângulo. Paralelogramo é um quadrilátero que possui os lados opostos paralelos. Retângulo possui quatro ângulos congruentes entre si. O losango possui quatro lados congruentes entre si, e finalmente o quadrado que possui 4 lados e quatro ângulos congruentes entre si.
GEOMETRIA ESPACIAL
A Geometria espacial (euclidiana) funciona como uma ampliação da Geometria plana (euclidiana) e trata dos métodos apropriados para o estudo de objetos espaciais assim como a relação entre esses elementos. Os objetos primitivos do ponto de vista espacial, são: pontos, retas, segmentos de retas, planos, curvas, ângulos e superfícies. Os principais tipos de cálculos que podemos realizar são: comprimentos de curvas, áreas de superfícies e volumes de regiões sólidas. Tomaremos ponto e reta como conceitos primitivos, os quais serão aceitos sem definição.
Conceitos gerais
Um plano é um subconjunto do espaço R3 de tal modo que quaisquer dois pontos desse conjunto pode ser ligado por um segmento de reta inteiramente contido no conjunto.
Um plano no espaço R3 pode ser determinado por qualquer uma das situações:
- Três pontos não colineares (não pertencentes à mesma reta);
- Um ponto e uma reta que não contem o ponto;
- Um ponto e um segmento de reta que não contem o ponto;
- Duas retas paralelas que não se sobrepõe;
- Dois segmentos de reta paralelos que não se sobrepõe;
- Duas retas concorrentes;
- Dois segmentos de reta concorrentes.
Duas retas são ditas reversas quando uma não tem interseção com a outra e elas não são paralelas. Pode-se pensar de uma rera r desenhada no chão de uma casa e uma reta s desenhada no teto dessa mesma casa.

Uma reta é perpendicular a um plano no espaço R3, se ela intersecta o plano em um ponto P e todo segmento de reta contido no plano que tem P como uma de suas extremidades é perpendicular à reta.

Uma reta r é paralela a um plano no espaço R3, se existe uma reta s inteiramente contida no plano que é paralela à reta dada.
Seja P um ponto localizado fora de um plano. A distância do ponto ao plano é a medida do segmento de reta perpendicular ao plano em que uma extremidade é o ponto P e a outra extremidade é o ponto que é a interseção entre o plano e o segmento.
Se o ponto P estiver no plano, a distância é nula.

Planos concorrentes no espaço R3 são planos cuja interseção é uma reta. Planos paralelos no espaço R3 são planos que não tem interseção.
Quando dois planos são concorrentes, dizemos que tais planos formam um diedro e o ângulo formado entre estes dois planos é denominado ângulo diedral. Para obter este ângulo diedral, basta tomar o ângulo formado por quaisquer duas retas perpendiculares aos planos concorrentes.

Planos normais são aqueles cujo ângulo diedral é um ângulo reto (90 graus).
AREAS EM QUE A GEOMETRIA PLANA E ESPACIAL FAZEM PARTE:
Envie agora
A Geometria Plana e a Geometria Espacial baseiam-se nos chamados conceitos geométricos primitivos. Define-se como conceito primitivo toda aquele que não admite definição, isto é, o conceito que é aceito por ser óbvio ou conveniente para uma determinada teoria. Normalmente, em Matemática, os conceitos primitivos servem de base para a construção de postulados (ou axiomas) que formarão, por sua vez, a estrutura lógica e formal da teoria.
Ao contrário do que se pensa, conceitos primitivos existem não somente em Matemática, mas em fisica também. Exemplos desses conceitos são os conceitos de força e velocidade.
Os conceitos geométricos primitivos são os seguintes:
- Ponto: é o conceito geométrico primitivo fundamental. Euclides o definiu como "aquilo que não tem parte". Ou seja, para Euclides é o conceito de "parte", e não de "ponto", que é primitivo.
- Imagine o ponto o menor que você puder. Diz-se que o ponto não tem dimensão (é adimensional), ou seja, ele é tão ínfimo quanto quisermos, e não faz sentido mencionar qualquer coisa sobre tamanho ou dimensão do ponto. A única propriedade do ponto é a localização.
- Representa-se o ponto por uma letra maiúscula qualquer do alfabeto latino.
- Linha: Imagine um pedaço de barbante sobre uma mesa, formando curvas ou nós sobre si mesmo: este é um exemplo de linha.
- Reta: É uma linha infinita e que tem uma única direção. Uma reta é o caminho mais curto entre dois pontos quaisquer.
- Superfície:
- Plano: Você pode imaginá-lo como uma folha de papel infinita. Um plano é uma superfície plana que se estende infinitamente em todas as direções.
Assinar:
Comentários (Atom)






